Netrix S.A.

Osiągniecie założonej liczby opracowanych modeli rozwiązania zagadnienia prostego.

Liczba opracowanych modeli numerycznych >=5
Każdy z opracowanych modeli spełnia również parametr:
Liczba elementów siatki przypadających na jeden model >= 500

1.    Model o elementach kwadratowych z elektrodami punktowymi - Siatka składa się z 5687 elementów kwadratowych
2. Model o elementach kwadratowych z elektrodami odcinkowymi - Siatka składa się z 5687 elementów kwadratowych
3. Model o elementach trójkątnych z elektrodami punktowymi - Model składa się z 1153 trójkątnych elementów
4. Model o elementach trójkątnych z elektrodami odcinkowymi - Model składa się z 1205 trójkątnych elementów
5. Model o elementach czworościennych z elektrodami punktowymi - Model składa się z 3347 czworościennych elementów
6. Model o elementach czworościennych z elektrodami powierzchniowymi - Model składa się z 4820 czworościennych elementów
7. Model o elementach sześciennych z elektrodami punktowymi - Siatka składa się z 26230 elementów sześciennych
8. Model o elementach sześciennych z elektrodami powierzchniowymi - Siatka składa się z 26230 elementów sześciennych

Osiągnięcie założonej liczby opracowanych modeli algorytmów rozwiązania zagadnienia odwrotnego z zastosowaniem sztucznych sieci neuronowych.

Opracowanie co najmniej 3 algorytmów rozwiązania zagadnienia odwrotnego w oparciu o oprogramowanie Matlab

Po przeprowadzeniu analizy możliwych rozwiązań dotyczących implementacji metod uczenia głębokiego i klasycznych sztucznych sieci neuronowych (Zadanie 2.1) przeprowadzono badania prowadzące do opracowania własnych algorytmów, częściowo wykorzystujących pomysły opisane w literaturze.

Na początku przeprowadzono eksperymenty wykorzystujące klasyczne sztuczne sieci neuronowe (Zadanie 2.3). Niestety wstępne wyniki tych eksperymentów (zweryfikowane wizualnie) były zbyt słabe aby kontynuować prace nad nimi dlatego też skupiono się nad rozwiązaniami wykorzystującymi uczenie głębokie.

W ramach przeprowadzonych prac opracowano 2 metody uczenia głębokiego (Zadanie 2.4), jedna z nich to hybryda złożona z warstw przetrenowanych autoenkoderów, a druga polega na korekcji obrazów rekonstrukcji wykonanej metodą deterministyczną za pomocą zmodyfikowanego modelu UNet. Obie te metody dają obiecujące wyniki.

W sumie opracowano 3 metody 1 wykorzystująca klasyczne sztuczne sieci neuronowe i 2 wykorzystujące uczenie głębokie, więc w tym aspekcie kamień milowy został spełniony.

Algorytmy opracowane poddane procesowi uczenia na zbiorze co najmniej 10 tys. syntetycznych danych pomiarowych

W ramach eksperymentów wygenerowano wiele różnych zbiorów danych, ostatecznie jednak opracowano zbiór danych podobny do danych rzeczywistych uzyskiwanych w laboratorium (Zadanie 2.2). Ten zbiór danych składa się ze 150 tysięcy próbek. Został on podzielony na zbiór treningowy składający się ze 120 tysięcy próbek i zbiór testowy składający się z 30 tysięcy próbek. Widzimy więc, że w tym aspekcie również założenia określone w kamieniu milowym zostały spełnione. Ostateczne dane zostały wykorzystane do treningu i testowania obu modeli wykorzystujących uczenie głębokie.

Dokładność działania algorytmu (rekonstrukcji) co najmniej 92%

Z 3 opracowanych algorytmów tylko 2 (te oparte o uczenie głębokie) zostały dalej rozwijane po wstępnych testach. Ostateczne ich wersje zostały zweryfikowane numerycznie za pomocą dwóch różnych metryk. Algorytm oparty o zmodyfikowany model UNet spełnia założenia zawarte w kamieniu milowym (wartości obu metryk są większe od 92%). W kamieniu milowym jest mowa o jednym algorytmie, który ma spełnić te założenia.

Omawiany algorytmy został napisane w języku Python z wykorzystaniem oprogramowania Matlab ze względu na możliwość jego uruchomienia na klastrze.

Osiągnięcie założonej liczby opracowanych modeli algorytmów rozwiązania zagadnienia odwrotnego z zastosowaniem metod statystycznych.

Trzeci Kamień Milowy dotyczy osiągnięcia założonej liczby opracowanych modeli algorytmów rozwiązania zagadnienia odwrotnego z zastosowaniem metod statystycznych. W przeciwieństwie do poprzedniego Kamienia Milowego, gdzie zastosowano sztuczne sieci neuronowe, metody statystyczne stawiają na krytyczną ocenę danych wejściowych i selekcję najistotniejszych cech dla uzyskania wyniku końcowego - rekonstrukcji.

Parametry:

1. Opracowanie co najmniej 2 algorytmów rozwiązania zagadnienia odwrotnego w oparciu o oprogram. Matlab©.
2. Algorytmy opracowane poddane procesowi uczenia na zbiorze co najmniej 10 tys. syntetycznych danych pomiarowych.
3. Dokładność rekonstrukcji na poziomie 95%. Czas działania nie może przekraczać 350ms.

1. Opracowane algorytmy

W toku prac przeprowadzono gruntowną analizę rozwiązań, modeli statystycznych oraz ich wymagań implementacyjnych. Szczegółowy opis zawarty jest w załączonym raporcie.

Po wykonaniu analizy opracowano dwa rodzaje algorytmów statystycznych do rozwiązywania zagadnienia odwrotnego w elektrycznej tomografii impedancyjnej

- Opracowano modelu algorytmu rekonstrukcji metody LARS i

- Opracowano modelu algorytmu rekonstrukcji z zastosowaniem metody Elastic Net

Kody źródłowe opracowano w języku Python z wykorzystaniem środowiska Matlab.

2. Dane

Algorytmy poddano uczeniu na przygotowanym wcześniej zbiorze danych. Na potrzeby metod statystycznych przygotowano zbiór 40 tys. danych syntetycznych. Według potrzeb konkretnego algorytmu z tego zbioru losowano podzbiór o wielkości co najmniej 10 tys. punktów do wykonania procesu uczenia. Wykorzystana ilość danych spełnia wymagania Kamienia Milowego.

3. Dokładność

Używając  zdefiniowanej dokładności rekonstrukcji otrzymujemy wyniki na poziomie 95%-98% w zależności od algorytmu oraz konkretnego przypadku. Wynik ten spełnia założenia Kamienia Milowego.

Czas wykonania algorytmu wynosi mniej niż 100ms, co również spełnia postawione wymogi.

Osiągnięcie założonej liczby przygotowanych syntetycznych danych pomiarowych.

Liczba przygotowanych syntetycznych danych pomiarowych, dla każdej z zastosowanych metod >= 10000

W trakcie prac nad symulacjami wygenerowano ponad 200 tysięcy danych, z czego do uczenia algorytmów rozwiązywania zagadnienia odwrotnego wyselekcjonowano zbiór 150 tys. oraz 40 tys. na potrzeby nauki odpowiednio sztucznych sieci neuronowych i modeli statystycznych.

Opracowanie danych syntetycznych do uczenia i walidacji działania algorytmów opracowanych w oparciu o sztuczne sieci neuronowe i metody statystyczne

Opis działania algorytmu symulacyjnego stanowi: “Podzielenie wygenerowanych danych syntetycznych na zbiory - treningowy i testowy”. Oznacza to, że każdy zbiór danych syntetycznych został podzielony na zbiór treningowy (do uczenia) służący do uczenia algorytmów opracowanych w oparciu o sztuczne sieci neuronowe oraz metod statystycznych. Obok został wydzielony także zbiór testowy (walidacji), służący do weryfikacji i oceny pracy wyuczonych algorytmów.

Dane opracowane z wykorzystaniem oprogram. Matlab©

Omawiany skrypt został napisany w języku Python z wykorzystaniem oprogramowania Matlab ze względu na możliwość jego uruchomienia na klastrze. Jednakże kod ten został przygotowany (oraz można go bez problemu wykonać) w środowisku Matlab.

Osiągnięcie założonej liczby opracowanych modeli rozwiązania zagadnienia prostego

Liczba opracowanych modeli numerycznych >=5 Liczba elementów siatki przypadających na jeden model >= 650 Uwzględnienie zmian geometrii dla każdego z modeli >= 5% powierzchni. Uwzględnienie rozmieszczenia i rozmiaru elektrod. Modele przygotowane w oparciu o oprogram. Matlab®.

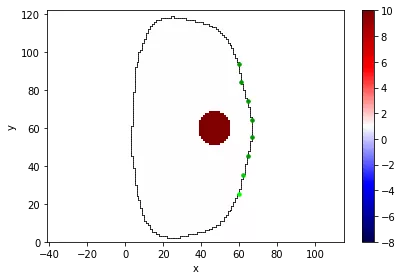
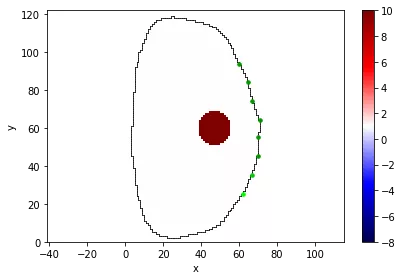
Modele opracowane na danym etapie projektu pozwalają na wykonanie obliczeń symulacyjnych opierających się na rozwiązaniu problemu prostego. W przeprowadzonych pracach stworzone modele zostały przystosowane do metody pomiarowej EIT (elektryczna impedancyjna tomografia). Utworzono ponad 5 modeli numerycznych w postaci siatek geometrycznych, tym samym spełniając kryteria kamienia milowego. Każdy z utworzonych modeli zakłada liczbę elementów skończonych powyżej 650, np. na Rys. 2 pokazano model składający się z 6243 elementów skończonych. Dodatkowo spełnione zostało założenie o zmianie powierzchni siatek, model przedstawiony na Rys. 2 został utworzony na podstawie siatki pokazanej na Rys.1 poprzez zwiększenie powierzchni o 10% względem oryginału. Tworząc modele w tym etapie projektu zadbano także o implementację rodzaju elektrod. W każdym z modeli istnieje możliwość zamiany elektrod punktowych na elektrody odcinkowe, które pozwala na symulację powierzchni elektrod pomiarowych występujących w rzeczywistym pomiarze. W ramach prac opracowano i zaimplementowano siatki geometryczne, których przykłady zostały przedstawione na poniższych rysunkach:

Osiągnięcie założonej liczby opracowanych modeli algorytmów rozwiązania zagadnienia odwrotnego z zastosowaniem sztucznych sieci neuronowych.

Osiągnięte parametry kamienia milowego: liczba opracowanych algorytmów >=3,wskaźnik średniej kwadratowej błędu predykcji (RMSE)<=0,5, opracowane algorytmy będą w stanie dokonać rekonstrukcji obrazu w czasie nie gorszym niż 300 ms przy zachowaniu dokładności na poziomie 95%, algorytmy zostaną opracowane z zastosowaniem oprogramowania Matlab.

W ramach kamienia milowego opracowano 3 algorytmy: zmodyfikowany model UNet, model hybrydowy oraz płytkiej sieci neuronowej typu fully connected.

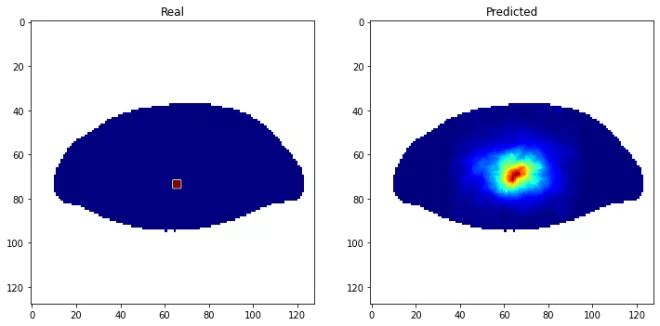
Szczegóły osiągniecia kamienia milowego, znajdują się w dokumencie opisującym kamień milowy. Poniżej przedstawione przykładowe wyniki uzyskane za pomocą algorytmów.

Osiągnięcie założonej liczby opracowanych modeli algorytmów rozwiązania zagadnienia odwrotnego z zastosowaniem metod statystycznych

• Liczba opracowanych algorytmów >=2  
• Wskaźnik średniej kwadratowej błędu predykcji (RMSE) <= 0,5 
• Opracowane algorytmy będą w stanie dokonać rekonstrukcji obrazu w czasie nie gorszym niż 300 ms przy zachowaniu dokładności na poziomie 97%.  
• Algorytmy zostaną opracowane z zastosowaniem oprogram. Matlab.  

Rozwiązanie zagadnienia odwrotnego w projekcie zostało opracowane przy pomocy następujących modeli z zastosowaniem metod statystycznych: Regresja lasso, Elastic Net, Regresja grzbietowa.